Dimostrazioni e dimostratori

Recentemente sono apparse sulla scena matematica altri tipi di dimostrazioni, solo apparentemente riconducibili alle dimostrazioni "classiche". Sono uguali i metodi e in parte gli strumenti logici, ma c'è un'essenziale differenza, che rischia di essere considerata solo in termini di tempo, mentre è in termini più generali di "agente". Diciamo che l'essenza di queste nuove dimostrazioni è costituita dalla forza bruta, cioè dall'uso di calcolatori.

Il teorema dei quattro colori

Il primo esempio di questo nuovo corso è stato, nel 1977, la dimostrazione della congettura dei quattro colori (da lì in avanti chiamata "Teorema"). Questo fu il primo caso di utilizzo di un "esecutore di algoritmi non umano" utilizzato per risolvere un problema; la dimostrazione completa, così ottenuta, è di circa 500 pagine e, dalle cronache della dimostrazione, variamente riportate in rete, appare che il calcolatore non servì solo a "mandare in macchina" calcoli lunghi e complessi ma aiutò anche la fase stessa di riformulazione delle ipotesi euristiche.

In poche parole si tratta di questo:

Quanti colori sono necessari per colorare una mappa piana, costituita da regioni connesse, facendo in modo che due regioni che confinano per almeno un segmento non siano colorate dello stesso colore?

Pare che il primo a formulare la congettura (cioè a ipotizzare che la risposta alla domanda fosse: «quattro») sia stato nel 1852 Francis Guthrie, uno studente di Augustus De Morgan. Ma la congettura tale è rimasta, nonostante i tentativi di dimostrazione (o, meglio, le dimostrazioni fornite da matematici, poi rivelatasi non corrette) fino alla fine del XX secolo. A questo punto l'approccio che fu tentato da Kenneth Appel e Wolfgang Haken fu quello di passare attraverso la classificazione delle casistiche possibili, rilevando che sono in numero finito (cioè rappresentabili con un numero finito di grafi) vale rappresentabili con 1.476 grafi possibili.

A questo punto i due matematici hanno rilevato che dimostrare manualmente il teorema corrispondeva a fornire 1.476 soluzioni a problemi parziali, che, tutte insieme, esaurissero tutti gli aspetti possibili del problema generale. E che per determinare e attestare 1.476 dimostrazioni occorreva "una mano"...

Jean Gillot

A prima vista potrebbe sembrare una fisima il non voler affidare i noiosi calcoli a un computer; del resto, Jean Gillot, che fu prima servitore e poi allievo di Cartesio, veniva "utilizzato" da questi per risolvere le dispute matematiche. Cartesio non interveniva in prima persona nelle dispute con gli studiosi dell'epoca per dimostrare l'efficacia del suo metodo; al suo posto inviava il "servitore" che riusciva, con sorprendente facilità, a mostrare l'efficacia del metodo analitico nella risoluzione dei problemi, costituendo, in tal senso, il primo esempio di "calcolatore". Ma allora perché non fare lo stesso anche quattro secoli dopo, tanto più con oggetti ai quali non servirà nemmeno, in seguito, come premio delle loro fatiche, procurare il posto di Matematico ufficiale del Portogallo?

Il problema logico filosofico forse più importante che occorre valutare consiste nel fatto che i computer, a ben vedere, non dimostrano affatto un teorema. I calcolatori eseguono un algoritmo, ottenendone un risultato. La dimostrazione si ricombina poi ad opera di un matematico che rileva il risultato dell'algoritmo eseguito e ne deduce passi essenziali o essenzialmente impegnativi in termini di tempo e di fatica per dimostrare la tesi iniziale.

La discesa tortuosa

Ma questa non è proprio la stessa cosa; perché stiamo affermando che il teorema T è dimostrato se il risultato R dell'algoritmo A è corretto. Cioè 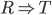o, meglio ancora .

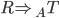Ma la domanda ovvia, a questo punto è: chi garantisce che l'algoritmo sia corretto? E qui l'affare si complica un tantino, dato che l'algoritmo in realtà non è un concetto unico: esiste l'algoritmo descritto dal matematico, quindi la sua versione espressa, diciamo, in pseudolinguaggio (cioè in un linguaggio artificiale, non necessariamente un linguaggio di programmazione, atto a rappresentare compiutamente tutti i concetti che occorrono per fornire le istruzioni operative che devono essere eseguite da parte del calcolatore). Ma, dopo questo esiste la traduzione dello pseudocodice nel linguaggio comprensibile, questa volta, all'ambiente di esecuzione gestito nel calcolatore. E infine il linguaggio macchina vero e proprio, la successione cioè di istruzioni che il calcolatore, con il suo sistema operativo e il suo hardware, può effettivamente eseguire. Ricapitolando si ha quindi:

Algoritmo in linguaggio naturale 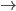Algoritmo in pseudocodice 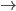Algoritmo interpretato 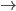Algoritmo compilato in linguaggio macchina 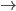Singola istanza del programma in esecuzione

La condizione necessaria quindi perché valga T diventa che nessuno dei passaggi indicati dalle frecce perda o alteri informazioni o significato. E se questo sembra un dato marginale fino a quando il calcolatore è solo una facilitazione in quanto permette di ottenere prima risultati poi verificabili (almeno in linea teorica) manualmente da parte di umani, che dire di risultati che non ci sarebbe nemmeno il tempo fisico di "ri-"dimostrare manualmente?

Immaginiamo (ma la cosa non richiede una fantasia eccessiva) un teorema di teoria dei numeri. Un teorema che riguardi le proprietà di un numero primo di un numero piuttosto sostenuto di cifre, diciamo di un milione di cifre. E ipotizziamo anche che esista un algoritmo che possa dimostrarlo, ma che per essere eseguito necessiti direi di: cento anni di una persona oppure di qualche secondo (o ora, o giorno, non importa) di un calcolatore. Potremmo considerare un teorema "dimostrato" in queste condizioni?

Ricordiamo una acquisizione recente della nostra civiltà, questa sì per opera della grande accelerazione impressa dai computer al nostro modo di concepire il mondo:

Non è pensabile di salvare un documento in quanto tale per un tempo indefinito; l'unica cosa che si può sperare di conservare è l'informazione, all'interno del contesto in cui ha senso.

Questo essenzialmente suggerisce perché dopo cento anni nessuno sarebbe più intento a dimostrare manualmente quel teorema; anche se il teorema, come informazione, avrebbe ancora significato.