Dopo i due passaggi iniziali, di formulazione del quesito e di prime risposte parziali, eccoci ora fra le mani, dopo alcuni viaggi, al mattino, sui treni delle Ferrovie Nord Milano, la congettura di una possibile soluzione alla nostra risposta. Vediamo ora tanto la congettura quanto la sua validità nei casi particolari analizzati fino ad ora. Si tratta di questa formula
dove:
è l'insieme dei multipli di 
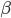tali che nessun 
sia mutiplo di un 
In particolare, dato un intero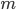 
, questo è scomponibile come 
con 
elevati ai relativi esponenti. Quindi, nella definizione di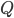 
, le coppie di elementi 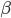e 
saranno da intendersi come:
con 
della scrittura di scomposizione in fattori di .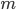
Riduzione delle formule nei casi precedenti
Prima di considerare la dimostrazione della nostra formula generale, vediamola applicata nei casi particolari da cui siamo partiti.
Consideriamo il primo caso, quello in cui 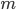è un numero primo. Ma allora: 
e quindi:
- se
allora 
e viceversa; ma anche: - se allora
;
quindi la formula generale diventa:
che, dopo qualche riduzione, ricordando che i "multipli" di 1 sono tutti gli elementi di riga, quindi 
diventa:
.
A parte la notazione, qui più precisa del caso iniziale, intendendo 
e ricordando che (dato che il quoziente di 1 è 
: (
)) la formula sopra, nel caso particolare,diventa:
.
cioè concide esattamente con quella dimostrata nel primo articolo.
Caso 
con 
primi diversi
Verifichiamo in questo ulteriore caso se la formula continua a valere. I numeri di cui dovremo interessarci saranno quelli per cui l'apporto alla sommatoria non sia nullo; in particolare avremo quattro addendi nella nostra sommatoria, quelli dati dagli elementi dell'insieme: 
.
Analizzando gli addendi separatamente avremo che il termine generico 
assumerà le seguenti forme:
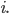
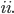
e, ricordando che valgono le seguenti riduzioni:
- dato che non esistono multipli di 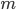strettamente inferiori a 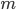(per definizione di 
);
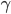otteniamo quindi:
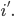
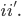
Ora, per alleggerire un poco la notazione, ricordando quanto già fatto nell'articolo precedente, facciamo un cambio di notazione in base alle convenzioni seguenti:
da cui le 
diventano
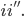
ma questi quattro addendi, dopo opportune semplificazioni, portano, sommati, alla formula:
.
E quindi: anche in questo caso otteniamo che la formula generale, precisata nella situazione corrente, coincide esattamente con quanto dimostrato in precedenza.
Caso 
con 
primo
Per concludere la casistica analizzata negli articoli precedenti, rimane il caso particolare di un . Ma i ragionamenti sono analoghi al caso precedente, salvo intendere che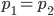 
e che gli addendi nella somma generale saranno 3 invece di 4. In particolare avremo questi addendi:
che, in notazione meno precisa ma più efficace diventano:
ma quindi:
Un calcolo per rendere meno ardua la formula iniziale...
Consideriamo ora il caso di voler trovare i multipli di 8 nella tavola pitagorica 
.
Procediamo nel calcolare la scomposizione in fattori; attenzione: non in fattori primi, ma semplicemente in fattori interi considerando anche 1. Otteniamo che i fattori sono: 1, 2, 4 e 8.
Chiaramente i quozienti di questi quattro numeri rispetto a 20 saranno: 
,
,
e 
. Ricordando la regola espressa dalla formula, vediamo quali sono i 4 addendi da considerare:
(N.B.: 
e 
sono multipli di 
e non vanno considerati)
(N.B.: è multiplo di e non va considerato)
che portano a 
.
E' semplice impostare in un foglio di calcolo come OpenOffice Calc una griglia di risultati di moltiplicazione su cui verificare che il calcolo sia corretto.